
The renewed interest in safety issues for large scale industrial devices and in high speed combustion has driven recent intense efforts to gain a deeper theoretical understanding of detonation wave dynamics. of Civil Engineering OSTI Identifier: 6745637 Report Number(s): NUREG/CR-2897 ON: DE83900138 Resource Type: Technical Report Resource Relation: Other Information: Portions of document are illegible Country of Publication: United States Language: English Subject: 22 GENERAL STUDIES OF NUCLEAR REACTORS 21 SPECIFIC NUCLEAR REACTORS AND ASSOCIATED PLANTS BWR TYPE REACTORS CONTAINMENT BUILDINGS DETONATIONS PRESSURE GRADIENTS PWR TYPE REACTORS COMPUTER CALCULATIONS EXPLOSIONS HYDROGEN MATHEMATICAL MODELS REACTOR SAFETY CONTAINMENT ELEMENTS NONMETALS REACTORS SAFETY WATER COOLED REACTORS WATER MODERATED REACTORS 220900* - Nuclear Reactor Technology- Reactor Safety 210100 - Power Reactors, Nonbreeding, Light-Water Moderated, Boiling Water Cooled 210200 - Power Reactors, Nonbreeding, Light-Water Moderated, Nonboiling Water = , Publication Date: Research Org.: Massachusetts Inst.
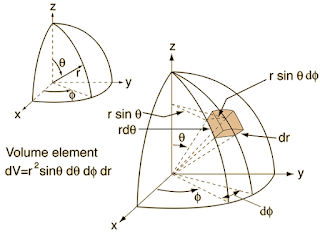
Dimensions were similar to the ones of the containment of the Indian Point Nuclear Power Plant.Īuthors: Delichatsios, M.
Calc 3 spherical coords fins phi code#
The two-dimensional axisymmetric code was used to calculate pressure time histories at the wall of a cylindrical containment capped with a semi-spherical dome. The one-dimensional code was modified to include coupling with an elastically deformable wall and the modified version was used to demonstrate that for typical concrete containment structures interaction of the waves with wall deformations has insignificant effects on the wave properties, and can be neglected. Numerical results for one-dimensional geometries show good agreement with available analytical solutions.

The detonation front is represented in the model as a discontinuity which changes the still unburnt gas to a completely burnt one, according to the Chapman-Jouguet conditions. The computational method is based on the Random Choice Technique which can handle accurately sharp discontinuities. Computer codes which simulate hydrogen detonators in planar, cylindrical, spherical and two-dimensional axisymmetric geometries have been developed.


 0 kommentar(er)
0 kommentar(er)
